SEGUIR
SEGUINDO
Resumindo a grande notícia matemática de hoje: descobriram um número muito grande. “E daí?”, você dirá. Vamos lá. O primeiro passo é apresentá-lo.
Abaixo, você vê os números de Dedekind. Trata-se de uma sequência obscura de números inteiros, nos mesmos moldes das famosas sequências de Fibonacci (0, 1, 1, 2, 3, 5, 8, 13..) ou dos números primos (2, 3, 5, 7, 11, 13…). Note que ela cresce bem rápido. Pula dos 7 mil para os 7 milhões em um único passo.
2
3
6
20
168
7.581
7.828.354
2.414.682.040.998
56.130.437.228.687.557.907.788
Agora, descobriram o décimo membro da sequência. Ou melhor, o nono: o 2 não conta, por motivos que vamos entender. É o gigante aí embaixo, com 42 dígitos. Ele demorou 32 anos para sair do forno. E representa um passo importante na maneira como matemáticos usam supercomputadores.
286.386.577.668.298.411.128.469.151.667.598.498.812.366
Toda sequência segue um padrão, naturalmente. Na de Fibonacci, cada número é a soma dos dois números anteriores. Os primos, por sua vez, são números que só podem ser divididos por si mesmos e por um, e não há uma fórmula conhecida para gerá-los, o que os torna um dos grandes mistérios da matemática. Entenda melhor neste texto.
(Digressão rápida: existe uma coleção online inteirinha dedicada a armazenar sequências como essas, para a alegria dos CDFs de plantão. Acesse aqui se estiver curioso.)
Qual, então, é a lógica por trás da sequência de Dedekind? Ela tem a ver com coisas chamadas funções boleanas monótonas, e a palavra “monótono” já dá uma boa ideia do que está por vir, rs.
Funções são pequenas engenhocas que engolem um número e cospem outro, sempre seguindo uma regra fixa. Por exemplo: se sua função consiste em multiplicar todos os números do universo por dois, então o três vira seis e o quatro vira oito.
“Monótona” significa, grosso modo, que o número que essa função cospe sempre cresce se você aumentar o número inserido. É o caso da função que usamos de exemplo no parágrafo aí em cima. Toda vez que o input cresce (2, 3, 4, 5…) o output da multiplicação por dois cresce junto (4, 6, 8, 10…).
Também dá para ser monótona se o número de saída sempre diminui conforme o número de entrada cresce. Nesse caso, temos uma função monótona decrescente. A definição tem outras sutilezas, mas não vamos nos ater a elas. O importante é: os números de Dedekind são gerados por uma função monótona crescente. E por isso, naturalmente, eles crescem. E como crescem!
O mais divertido é que o input é muito simples. 1, 2, 3, 4, 5, 6, 7, 8… Sinal de que alguma coisa rola nessa função. Alguma coisa tão maluca que, quando você insere o 8, ela cospe o 56.130.437.228.687.557.907.788 do outro lado.
O motivo desse Biotônico Fontoura algébrico é que, na função que gera a sequência de Dedekind, os números de entrada representam as dimensões espaciais. Uma, duas, três, quatro…
Sendo assim, vamos passar de dimensão em dimensão, entendendo como cada uma delas gera seu output, e por que os outputs vão aumentando tanto. É claro que não existem quatro ou cinco dimensões na prática, mas os matemáticos podem fazer contas com dimensões imaginárias, então não importa.
Começando esse “jogo” com uma dimensão só: uma linha reta, em pé na sua tela. O desafio é o seguinte: você precisa posicionar duas bolinhas, uma em cada ponta da linha. Uma bolinha é branca, a outra é vermelha. A vermelha precisa sempre ficar em cima da branca. E você pode por duas bolinhas brancas ou duas bolinhas vermelhas, se quiser (bem como uma de cada cor, é claro). Portanto, há três maneiras de fazer isso:
Aqui temos o primeiro par de input e output da função: input 1 (uma possibilidade) e output 3 (três possibilidades). O 3, portanto, é o primeiro dos números de Dedekind.
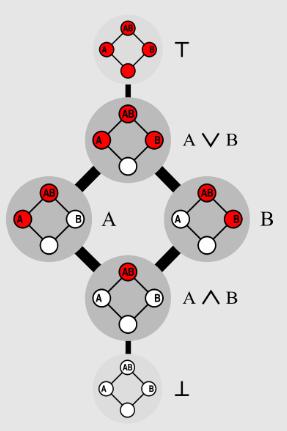
Agora, vamos pular para duas dimensões. Em vez de uma linha, teremos um quadrado. E há muito mais maneiras de distribuir as bolinhas seguindo essa regra quando se tem um quadrado. Mais precisamente, seis maneiras. É por isso que o segundo número de Dedekind é seis:
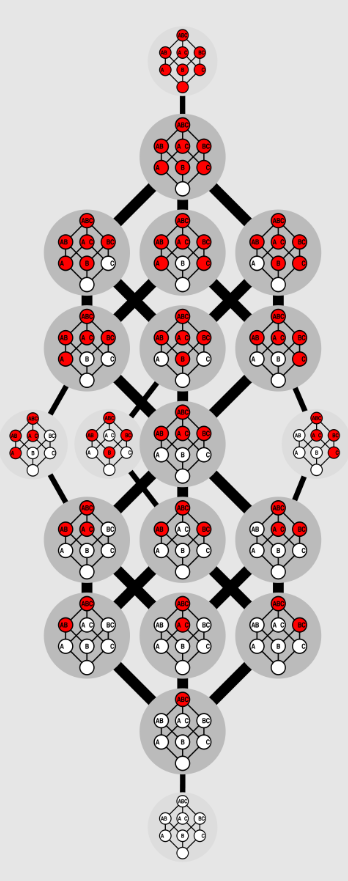
Agora, vamos para três dimensões. Com um cubo. Você já entendeu como funciona. Dessa vez, existem vinte possibilidades válidas. Portanto, o terceiro número de Dedekind é vinte.
Não é possível ilustrar a quarta, a quinta ou sexta dimensão. Mas pode confiar: há 168 disposições possíveis para os cubos de quatro dimensões (chamados tesseracts), 7.581 para os cubos de cinco dimensões, e por aí vai. O primeiro número de Dedekind, o 2, equivale às possibilidades para zero dimensões. Daí ele não entrar na sequência.
Conforme alcançamos dimensões mais altas, o cálculo fica muito difícil. O número para oito dimensões saiu do forno em 1991. E desde então, os matemáticos se perguntavam como diabos seria possível determinar o número de possibilidades para a nona dimensão.
O feito foi possível com um supercomputador chamado Noctua, localizado na Universidade Paderborn, na Alemanha. Quem deu início ao cálculo, três anos atrás, foi o aluno de mestrado Lennart Van Hirtum (que, desde que começou a investigação, já tirou suas titulações e virou pesquisador em tempo integral).
Seu orientador, Patrick De Causmaecker, criou a técnica que permite “picar” a conta de maneira a torná-la mastigável por um computador. Por meio de seu método, um PC doméstico comum consegue calcular o número de Dudekind na oitava dimensão, com 23 dígitos, em oito minutos.
Porém, quando subimos para o número de 42 dígitos da nona dimensão, o tempo vai para os milhares de anos. A capacidade de processamento de um desktop só não dá conta do recado.
Para piorar, os computadores de processamento paralelo mais potentes que existem nos datacenters de hoje (movidos por placas da Nvidia chamadas GPUs, usadas no treinamento de IAs como o ChatGPT) não têm a arquitetura compatível com o algoritimo necessário para fazer essa conta.
O jeito foi usar um outro tipo de chip, chamado FPGA, que é o segredo por trás do computador Noctua. A computação levou cinco meses, e em 8 de março, saiu o resultado. As conclusões foram apresentadas oficialmente em uma palestra, em 27 de junho.
Ao longo do século 20, calcular números gigantescos foi uma ferramenta importante para testar supercomputadores e inspirar novas arquiteturas de hardware e software. O trabalho de Van Hirtum e Causmaecker pode existir, por ora, no plano mais etéreo da matemática pura. Mas, amanhã, pode ser o segredo por trás de uma nova revolução em algum campo relevante da ciência da computação. A teoria anda para a prática poder correr.
ACESSO LIVRE COM VIVO FIBRA